|
|
|
| Lineare Funktionen - Schnittpunkt |
f1(x) = m1 ·
x + b1 und f2(x) = m2
· x + b2
|
Soll man den Schnittpunkt von zwei
Geraden bestimmen, ist jedem klar, dass man die Funktionsgleichungen
gleichsetzen muss.
So genau erklären warum kann ein Schüler normalerweise
nicht. Irgendwie sind die da eben gleich, die Geraden.
Gesucht ist genaugenommen das x, bei dem die Funktionswerte
beider Geraden identisch sind, denn das bedeutet, dass
die Punkte der Geraden an der Stelle übereinstimmen.
Für dieses x muss also gelten:
| |
f1(x) = f2(x) |
Gern und formal
schöner auch f1(xs) = f2(xs)
Ergebnis - eleganter:
xs = (b2 - b1) : (m1
- m2 )
ys = f1/2(xs) und S(xs;ys) |
| <=> |
m1 · x + b1 = m2
· x + b2 |
| <=> |
m1 · x - m 2
· x = b2 - b1 |
| <=> |
(m1 - m2 ) · x =
b2 - b1 |
| <=> |
x = (b2 - b1) : (m1
- m2 ) |
Die Scherzkekse unter den Schülern behaupten an
dieser Stelle oft, das sei der Schnittpunkt.
Es muss aber auch noch der beiden Funktionen gemeinsame
Funktionswert bestimmt werden. Theoretisch ist es egal,
welche der beiden Funktionen man hierzu verwendet.
(Praktisch oft nicht, da Rechenfehler
gern vorkommen)
|
Beispiel
Drücken wir uns nicht um ein Beispiel:
f1(x) = -3 · x + 18
f2(x) = 1,5 · x - 45
| |
f1(x) = f2(x) |
|
| <=> |
-3 · x + 18 = 1,5
· x - 45 |
| - 1,5 x |
| <=> |
-4,5 · x + 18 = -45 |
| - 18 |
| <=> |
-4,5 · x = -63 |
| : (- 4,5) |
| <=> |
x = 14 |
|
| |
einsetzen in f1 |
|
| |
f1(14) = -3 · 14 + 18 = -24 |
|
| |
(Probe: f2(14) = 1,5 ·
14 - 45 = -24) |
|
| also: |
S ( 14 ; -24 ) |
|
|
 |
|

| Präzision!!! |
Ich benutze die Begriffe Gerade, lineare
Funktion und Geradengleichung in der Tat etwas nachlässig.
Seis drum. |

| Hilfen |
| Javascriptseite;
Eingabe der m/b von zwei Geraden liefert den Schnittpunkt.
Tabellenkalkulation;
*.xls
(Micro$oft, 29k) ..
(simpel, mit Skizze) |

|
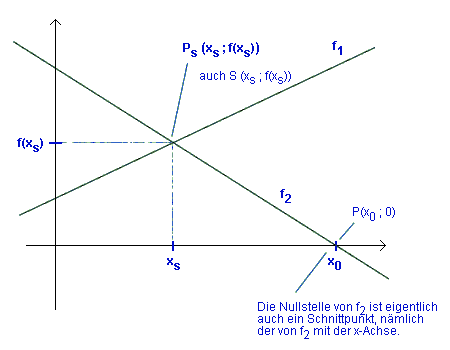
| Bemerkung zur Nullstelle
Die Nullstelle ist natürlich einerseits der x-Wert
(Stelle), an der der y-Wert einer Funktion =0 ist.
Eigentlich ist das, was man im KOS
sieht ein Punkt, nämlich der Schnittpunkt der Funktion
f mit der x-Achse.
Der Ansatz ist also hier
| f1(x) = m ·
x + b; f2(x) = 0 (die x-Achse) |
| |
f1(x) = f2(x) |
|
| <=> |
m · x + b = 0 |
|
| <=> |
x = - (b/m) |
|
| |
der bekannte Ansatz |
|
|
|
|
|